Partition and Shuffle
This work is supported by Continuum Analytics and the XDATA Program as part of the Blaze Project
This post primarily targets developers.
tl;dr We partition out-of-core dataframes efficiently.
Partition Data
Many efficient parallel algorithms require intelligently partitioned data.
For time-series data we might partition into month-long blocks. For text-indexed data we might have all of the “A”s in one group and all of the “B”s in another. These divisions let us arrange work with foresight.
To extend Pandas operations to larger-than-memory data efficient partition algorithms are critical. This is tricky when data doesn’t fit in memory.
Partitioning is fundamentally hard
Data locality is the root of all performance
-- A Good Programmer
Partitioning/shuffling is inherently non-local. Every block of input data needs to separate and send bits to every block of output data. If we have a thousand partitions then that’s a million little partition shards to communicate. Ouch.
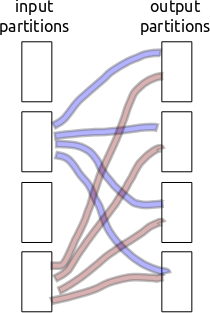
Consider the following setup
100GB dataset
/ 100MB partitions
= 1,000 input partitions
To partition we need shuffle data in the input partitions to a similar number of output partitions
1,000 input partitions
* 1,000 output partitions
= 1,000,000 partition shards
If our communication/storage of those shards has even a millisecond of latency then we run into problems.
1,000,000 partition shards
x 1ms
= 18 minutes
Previously I stored the partition-shards individually on the filesystem using cPickle. This was a mistake. It was very slow because it treated each of the million shards independently. Now we aggregate shards headed for the same out-block and write out many at a time, bundling overhead. We balance this against memory constraints. This stresses both Python latencies and memory use.
BColz, now for very small data
Fortunately we have a nice on-disk chunked array container that supports append in Cython. BColz (formerly BLZ, formerly CArray) does this for us. It wasn’t originally designed for this use case but performs admirably.
Briefly, BColz is…
- A binary store (like HDF5)
- With columnar access (useful for tabular computations)
- That stores data in cache-friendly sized blocks
- With a focus on compression
- Written mostly by Francesc Alted (PyTables) and Valentin Haenel
It includes two main objects:
carray: An on-disk numpy arrayctable: A named collection ofcarraysto represent a table/dataframe
Partitioned Frame
We use carray to make a new data structure pframe with the following
operations:
- Append DataFrame to collection, and partition it along the index on
known block divisions
blockdivs - Extract DataFrame corresponding to a particular partition
Internally we invent two new data structures:
cframe: Likectablethis stores column information in a collection ofcarrays. Unlikectablethis maps perfectly onto the custom block structure used internally by Pandas. For internal use only.pframe: A collection ofcframes, one for each partition.
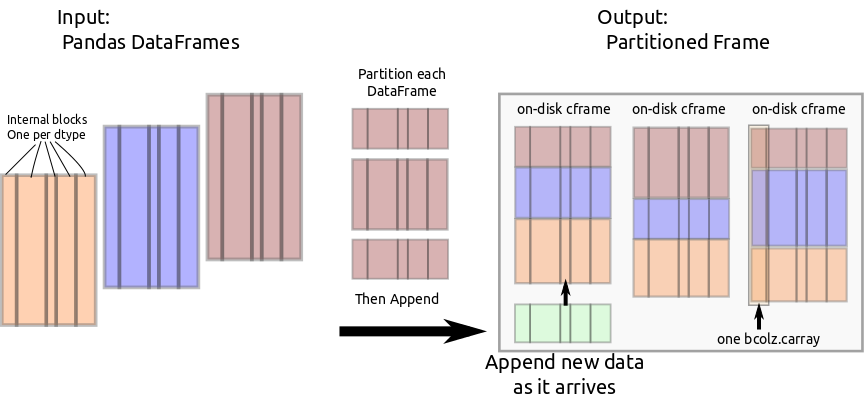
Through bcolz.carray, cframe manages efficient incremental storage to disk.
PFrame partitions incoming data and feeds it to the appropriate cframe.
Example
Create test dataset
In [1]: import pandas as pd
In [2]: df = pd.DataFrame({'a': [1, 2, 3, 4],
... 'b': [1., 2., 3., 4.]},
... index=[1, 4, 10, 20])Create pframe like our test dataset, partitioning on divisions 5, 15. Append
the single test dataframe.
In [3]: from pframe import pframe
In [4]: pf = pframe(like=df, blockdivs=[5, 15])
In [5]: pf.append(df)Pull out partitions
In [6]: pf.get_partition(0)
Out[6]:
a b
1 1 1
4 2 2
In [7]: pf.get_partition(1)
Out[7]:
a b
10 3 3
In [8]: pf.get_partition(2)
Out[8]:
a b
20 4 4Continue to append data…
In [9]: df2 = pd.DataFrame({'a': [10, 20, 30, 40],
... 'b': [10., 20., 30., 40.]},
... index=[1, 4, 10, 20])
In [10]: pf.append(df2)… and partitions grow accordingly.
In [12]: pf.get_partition(0)
Out[12]:
a b
1 1 1
4 2 2
1 10 10
4 20 20We can continue this until our disk fills up. This runs near peak I/O speeds (on my low-power laptop with admittedly poor I/O.)
Performance
I’ve partitioned the NYCTaxi trip dataset a lot this week and posting my results to the Continuum chat with messages like the following
I think I've got it to work, though it took all night and my hard drive filled up.
Down to six hours and it actually works.
Three hours!
By removing object dtypes we're down to 30 minutes
20! This is actually usable.
OK, I've got this to six minutes. Thank goodness for Pandas categoricals.
Five.
Down to about three and a half with multithreading, but only if we stop blosc from segfaulting.
And thats where I am now. It’s been a fun week. Here is a tiny benchmark.
>>> import pandas as pd
>>> import numpy as np
>>> from pframe import pframe
>>> df = pd.DataFrame({'a': np.random.random(1000000),
'b': np.random.poisson(100, size=1000000),
'c': np.random.random(1000000),
'd': np.random.random(1000000).astype('f4')}).set_index('a')Set up a pframe to match the structure of this DataFrame Partition index into divisions of size 0.1
>>> pf = pframe(like=df,
... blockdivs=[.1, .2, .3, .4, .5, .6, .7, .8, .9],
... chunklen=2**15)Dump the random data into the Partition Frame one hundred times and compute effective bandwidths.
>>> for i in range(100):
... pf.append(df)
CPU times: user 39.4 s, sys: 3.01 s, total: 42.4 s
Wall time: 40.6 s
>>> pf.nbytes
2800000000
>>> pf.nbytes / 40.6 / 1e6 # MB/s
68.9655172413793
>>> pf.cbytes / 40.6 / 1e6 # Actual compressed bytes on disk
41.5172952955665We partition and store on disk random-ish data at 68MB/s (cheating with compression). This is on my old small notebook computer with a weak processor and hard drive I/O bandwidth at around 100 MB/s.
Theoretical Comparison to External Sort
There isn’t much literature to back up my approach. That concerns me. There is a lot of literature however on external sorting and they often site our partitioning problem as a use case. Perhaps we should do an external sort?
I thought I’d quickly give some reasons why I think the current approach is theoretically better than an out-of-core sort; hopefully someone smarter can come by and tell me why I’m wrong.
We don’t need a full sort, we need something far weaker. External sort requires at least two passes over the data while the method above requires one full pass through the data as well as one additional pass through the index column to determine good block divisions. These divisions should be of approximately equal size. The approximate size can be pretty rough. I don’t think we would notice a variation of a factor of five in block sizes. Task scheduling lets us be pretty sloppy with load imbalance as long as we have many tasks.
I haven’t implemented a good external sort though so I’m only able to argue theory here. I’m likely missing important implementation details.
Links
- PFrame code lives in a dask branch at the moment. It depends on a couple of BColz PRs (#163, #164)
blog comments powered by Disqus